17.원주각 활용(쉬움)
안녕하세요 수학 공부 수공이에요 오늘은 원주각의 활용들을 배워보겠습니다.
쉽게 보는 각

원래 저번 편에서 설명해드리려고 했는 데 졸려가지고 지금 올리네요
사실 각도를 쉽게 구하는 법은 바로 호를 주의 깊게 보는 것인데요 .지금 이 사진에 있는 초록색 호가 공통인 호입니다.
이 공통인 호를 갖는 삼각형(한 변이 호인) 비슷한 것은 많은 종류들이 있는데 각을 구하기 위해서는 그 삼각형의 꼭짓덥이 어디있는 지를
잘 확인하면 쉽게 구할 수 있죠(만약 똑짓점이 원의 중심에 있다면 그것은 똑짓점이 원의 둘레의 있는 것의 2배겠죠 아님 그 반대거나)
아래는 예시들


그럼 이외의 꼭짓점은 어떻해?
이것도 증명이 필요하겠죠? 일단 예시를 보여주고 그 원리를 알려드리죠!
first. 형태

이것을 보아라 일단 같은 공통의 호를 초록색으로 표현하였다.

사실 호CD의 대한 원주각은 둘다 다름이 없다 이해가 안된다면 이걸 보자.

일단 파랑 색의 각도를 76도라고 하자 그럼 검은 색의 각도는 38도가 되겠지?
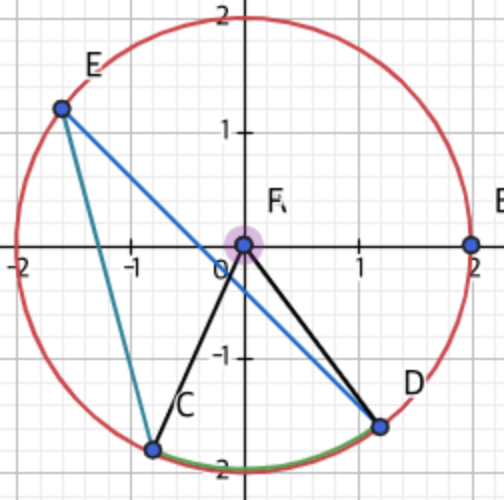
검은 색의 각도는 76도 그럼 파랑색의 각도도 38도가 되겠군
와우 이걸로 우리는 이 둘이 서로 같다는 것을 알았다 평생 이런 문제만 나왔으면 좋겠군 호호호
second 형태

원의 둘레 밖에 있는 보라색의 각도는 얼마일까? 어렵군 그래도 수공만 믿으라공!!

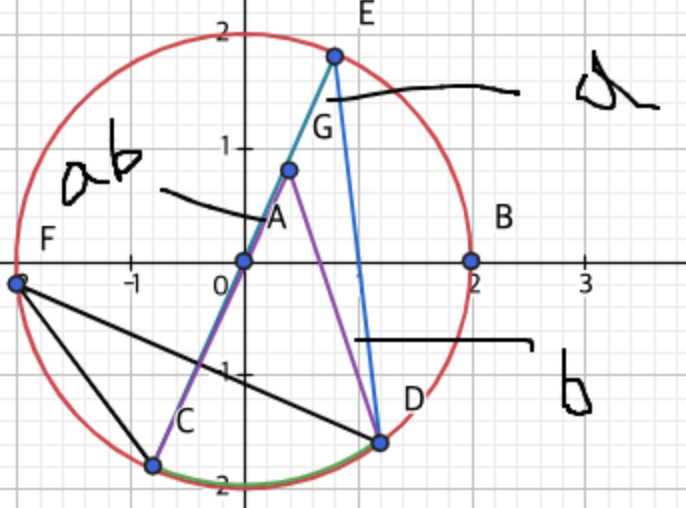
다들 한 외각의 크기는 이웃하지 않는 두 각의 합이랑 같다는 거 기억하죠 그것 때문에 파랑색 선의 각은 ab이고
뭐 딱히 설명할 것이 없어보이니 문제를 풀어보자

각 F는 30도이다. 보라색 선의 각은 20도이다, 각도 D는 얼마인가?
답: 각 F랑 각 E는 같으니까 , 각 E는 30도
각 E는 외각으로 다른 두 내각의 합이다. 내각 하나가 20이라고 써져 있으니 각 D는 10이다.
third, 형태

이것도 위에 거랑 원리가 비슷하다, 그러니 너무 놀라지 않기!
그렇다 사실 놀랄 것도 없었다. 이거 역시 두 내각은 다른 한 내각의 외각 같다는 공식이 제대로 쓰인 것이다.
이것도 문제를 풀면서 이해해 보도록 해요!
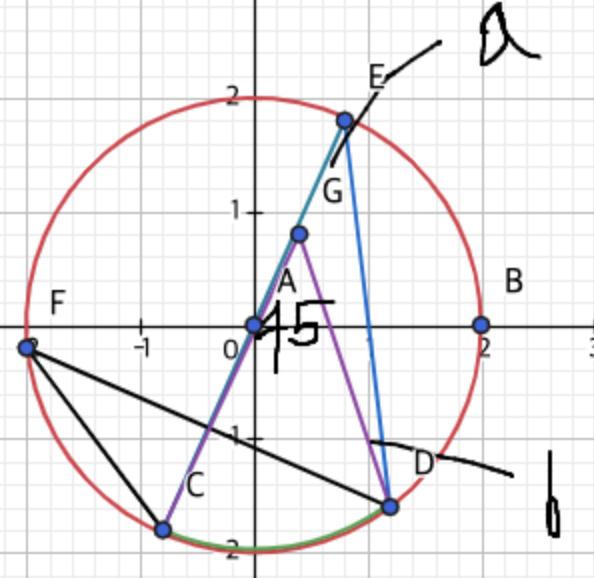
각 A는 45도, a와b의 각도비가 a : b = 1 : 2 라면 a,b의 각도는?
답은 a = 15, b = 30 왜냐하면 a + b는 45도 즉 45도에서 나누기 3을 하고 그걸 각 비에 대입하면 그 숫자가 나온다.
오늘도 수공이었습니다.
