안녕하세요 수학공부 수공이에요 오늘은 인수분해의 공식들을 알아봅시다!!
인수분해 공식
사실 인수분해의 공식은 별거 없습니다. 그저 다항식의 곱셈 공식을 반대로 한 것!!
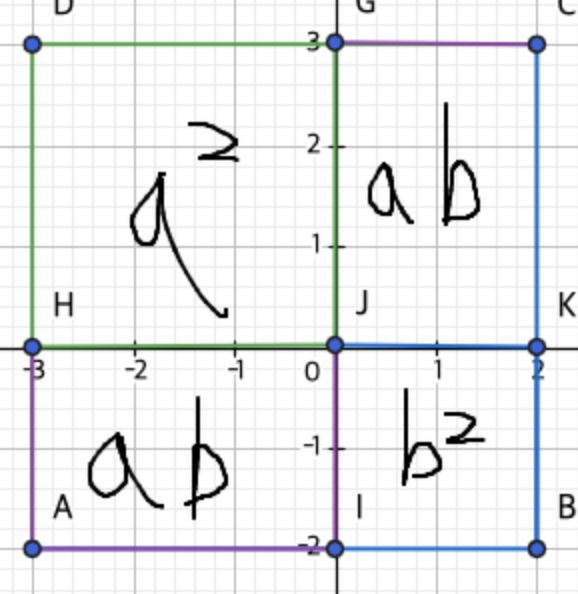
a²+ 2ab + b² = (a+b)² 이것의 이해를 위해서는 정사각형을 만들어야 한다.
어떤가 조금 이해가 가는지 잘 모르겠다 그러나 a² + 2ab + b²를 합치면 큰 정사각형의 넓이 공식
한 변 곱하기 다른 한변 그래서 a² + 2ab + b² = (a+b)²이 된다.
a²-b² = (b+a)(b-a)도 사진으로 이해해보자

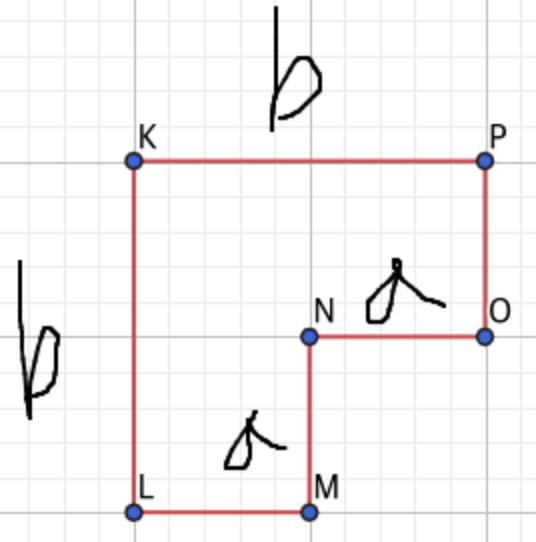
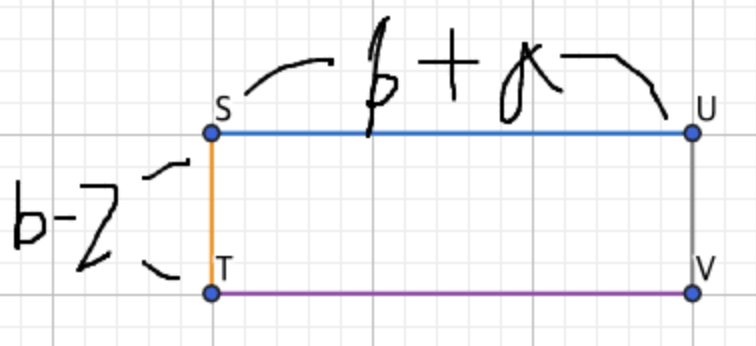
이렇게 보면 수학이 좀 재미있어지지 않나 b²(큰 정사각형) - a²(작은 정사각형) = 나머지 값을
짤라 긴 직사각형으로 만들고 (a+b)(a-b)의 값을 구해냈다. 와우
다음은 예제 몇개이다.
(1)16a² - 4. (2) a²+ 10a + 25. (3) 100a²+ 240 a +144 (4) 49a² + 28a + 4
(5)a² - 169 (6) a² + 1/4a + 1/64. (7) 16a² - 00.9.
이번엔 나머지 두개의 공식을 확인 해보자 화이팅
X² + (a+b)x +ab = (x+a)(x+b)
사진으로 이해해보자 이 사진에서 사용된 것은 X²+3X+2 =(X+1)(X+2)(출처:지학사 중3교과서)
(사진)
X²을 파란색 정사각형으로 만들고 1 x X 형태의 직사각형 3개를 x²에 붙이고 1을 1²이라는 정사각형으로 두개로
전체 직사각형의 빈 틈을 막아줬다. 훌륭한 수학적 발상인 것 같다.
그래서 결과적으로 (x+1)(x+2)라는 직사각형이 됐다.
이건 문제를 직접 풀어보자.
a²+ 6a + 8를 어떻게 푸느냐 정석 풀이법은 학교에서 배둘 것이니 여기서는 한 영상을 추천하겠다. 이 채널은 쉽게 쉽게 푸는 방법들을 알려주니 배워보자.
4. acx²+ (ad+bc)x + bd = (ax+b)(cx+d)
이건 푸는 방법을 알려주는 게 더 좋을 것 같아요.
예제 2x²-7x+3 (출처 지학사 중3수학)
a,b,c,d를 모두 찾아야 (ax+b)(cx+d)를 완성시킬 수 있어요.
우선 2x²에서 ac에 해당하는 부분은 2입니다 그 뜻은 ac = 2라는 소리죠 2는 2 x 1이고요
그 다음에 bd에 해당하는 숫자는 3이죠 3은 3 x 1,-3 x -1이죠
우리는 여기서 x자 곱하기를 해야해요 이 경우의 수를 보죠.
1. 2(a) \ /1(b) 2. 2(a) \ /-1(b) 3. 2(a) \ /3(b) 4. 2(a) \ /-3(b)
1(c) / \3(d) 1(c) / \-3(d) 1(c) / \1(d) 1(c) / \-1(d)
그리고 (ad+bc)에 해당하는 부분은 -7이죠 -7이 되게 하는 경우의 수는 2번
그래서 답은 2x²-7x+3 = (2x-1)(x-3) 끝